12 5 Equations Of Lines And Planes 2 2
12 5 Equations Of Lines And Planes We want to find a vector equation for the line segment between p and q. using p as our known point on the line, and − − ⇀ apq = x1 − x0, y1 − y0, z1 − z0 as the direction vector equation, equation 12.5.2 gives. ⇀ r = ⇀ p t(− − ⇀ apq). equation 12.5.3 can be expanded using properties of vectors:. Objectives:29. find the distance between a point and a plane.30. find the distance between a point and a line.31. find the distance between two parallel plan.

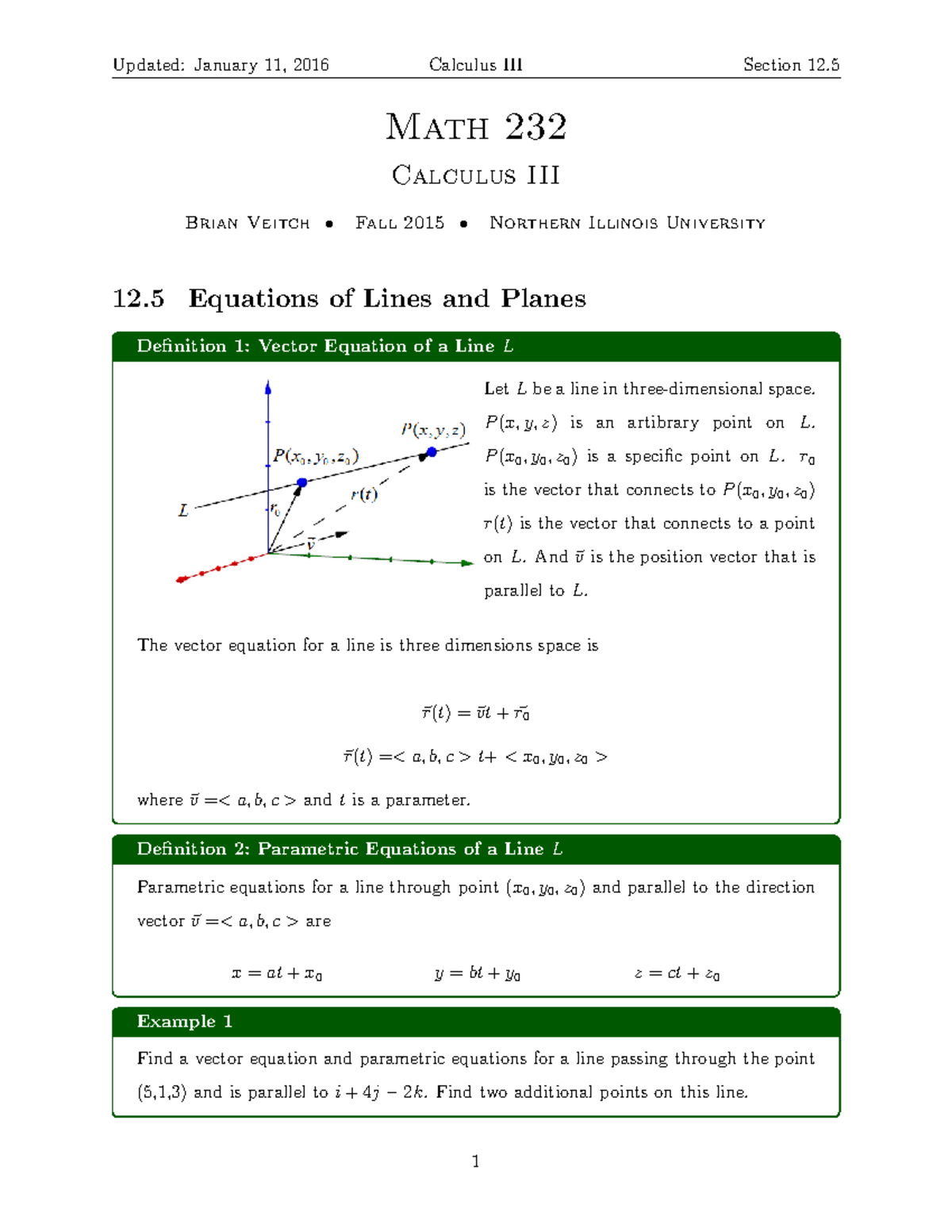
Sec 12 5 Pdf 12 5 Equations Of Lines And Planes Linesођ Solution. first, identify a vector parallel to the line: ⇀ v = − 3 − 1, 5 − 4, 0 − (− 2) = − 4, 1, 2 . use either of the given points on the line to complete the parametric equations: x = 1 − 4t y = 4 t, and. z = − 2 2t. solve each equation for t to create the symmetric equation of the line:. Vector equation of lines let l be a line through the point p 0 (reference point) and parallel to the vector v (direction vector). take an arbitrary point p on l, and let r 0 and r be the position vectors of p. My notes are available at asherbroberts (so you can write along with me).calculus: early transcendentals 8th edition by james stewart. Using the derivation above, the plane is 1x 2y 3z = 1 ⋅ 5 2 ⋅ 0 3 ⋅ 7 = 26. alternately, we know that the plane is x 2y 3z = d, and to find d we may substitute the known point on the plane to get 5 2 ⋅ 0 3 ⋅ 7 = d, so d = 26. example 12.5.2. find a vector normal to the plane 2x − 3y z = 15. solution.
12 5 Equation Of Lines And Planes Math 232 Calculus Iii Brian Veitch My notes are available at asherbroberts (so you can write along with me).calculus: early transcendentals 8th edition by james stewart. Using the derivation above, the plane is 1x 2y 3z = 1 ⋅ 5 2 ⋅ 0 3 ⋅ 7 = 26. alternately, we know that the plane is x 2y 3z = d, and to find d we may substitute the known point on the plane to get 5 2 ⋅ 0 3 ⋅ 7 = d, so d = 26. example 12.5.2. find a vector normal to the plane 2x − 3y z = 15. solution. Lines planes exercises exercises 1.find a set of vector, parametric, and symmetric equations of the line through the origin and the point (4;3; 1). 2.find a set of vector, parametric, and symmetric equations of the line through the point (0;14; 10) and parallel to the line x = 1 2t, y = 6 3t, z = 3 9t. Example 12.5.2 find a vector normal to the plane 2x − 3y z = 15. one example is 2, − 3, 1 . any vector parallel or anti parallel to this works as well, so for example − 2 2, − 3, 1 = − 4, 6, − 2 is also normal to the plane. . we will frequently need to find an equation for a plane given certain information about the plane.

Comments are closed.