Angle Bisector Theorem In A Triangle Proofs And Solved Examples Cuemath

By keluhanqu On Sep 20, 2024 Last updated

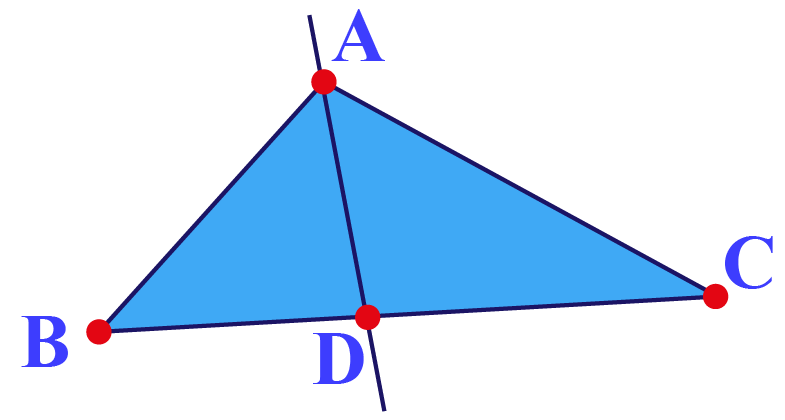
Angle Bisector Theorem In A Triangle Proofs And Solved Examples Cuemath The converse of angle bisector theorem states that if the sides of a triangle satisfy the following condition "if a line drawn from a vertex of a triangle divides the opposite side into two parts such that they are proportional to the other two sides of the triangle", it implies that the point on the opposite side of that angle lies on its angle bisector. The angle bisector in geometry is the ray, line, or segment which divides a given angle into two equal parts. for example, an angle bisector of a 60 degree angle will divide it into two angles of 30 degrees each. in other words, it divides an angle into two smaller congruent angles. given below is an image of an angle bisector of ∠aob.

Angle Bisector Theorem In A Triangle Proofs And Solved Examples Cuemath Solved examples on angle bisector theorem. go through the following examples to understand the concept of the angle bisector theorem. example 1: find the value of x for the given triangle using the angle bisector theorem. solution: given that, ad = 12, ac = 18, bc=24, db = x. according to angle bisector theorem, ad ac = db bc. Solved examples on perpendicular bisector theorem. example 1: in a pyramid, line segment ad is the perpendicular bisector of triangle abc on line segment bc. if ab = 20 feet and bd= 7 feet, find the length of side ac. solution. it is given that ad is the perpendicular bisector on the line segment bc. so, by perpendicular bisector theorem, any. Angle bisector theorem proof. statement: the angle bisector of a triangle divides the opposite side in such a way that the ratio of the two line segments is proportional to the ratio of the other two sides. let’s prove this statement. given: let us consider $\delta abc$, in which ad is the angle bisector of $\angle bac$, which meets bc at. Solution: by the angle bisector theorem, or . plugging this into and solving for ac gives . we can plug this back in to find . in triangle abc, let p be a point on bc and let . find the value of . solution: first, we notice that . thus, ap is the angle bisector of angle a, making our answer 0. part (b), 1959 imo problems problem 5.

Step into a world where your Angle Bisector Theorem In A Triangle Proofs And Solved Examples Cuemath passion takes center stage. We're thrilled to have you here with us, ready to embark on a remarkable adventure of discovery and delight.

Angle bisector theorem proof | Special properties and parts of triangles | Geometry | Khan Academy

Angle bisector theorem proof | Special properties and parts of triangles | Geometry | Khan Academy Angle bisector theorem examples | Geometry | Khan Academy Proof: The Angle Bisector Theorem The Triangle Angle Bisector Theorem Angle Bisector Theorem Angle Bisector Theorem - Midpoints & Line Segments Geometry - What is the triangle bisector theorem Using the Properties of the Triangle Angle Bisector Theorem to Determine Unknown Values Triangle Angle Bisector Theorem | MathHelp.com Introduction to Angle Bisectors of a Triangle Angle Bisectors in a Triangle | Don't Memorise Triangle Congruence Theorems, Two Column Proofs, SSS, SAS, ASA, AAS Postulates, Geometry Problems Triangle Angle Bisector Theorem - MathHelp.com - Math Help Altitudes, Medians, Midpoints, Angle & Perpendicular Bisectors WEEK 6: TRIANGLE ANGLE-BISECTOR THEOREM Angle Bisector | Theorem | Problems What is the Angle Bisector Theorem? (and Converse) Triangle Proportionality Theorem, Side Splitter Theorem & Angle Bisector Theorem - Geometry Prove: Angle Bisectors of a Triangle are Concurrent Constructing the Angle Bisectors of a Triangle

Conclusion

Delving deeply into the topic, one can conclude that the post delivers educational awareness on Angle Bisector Theorem In A Triangle Proofs And Solved Examples Cuemath. In the entirety of the article, the journalist illustrates significant acumen in the field. Crucially, the section on this point stands out as especially noteworthy. On top of that, the text is commendable in simplifying complex concepts in an straightforward manner. In addition, the blogger imparts actual cases that heighten the understanding. Another facet that marks this document as special is the thorough investigation of different aspects related to Angle Bisector Theorem In A Triangle Proofs And Solved Examples Cuemath. The commentators rigorous method affirms that perusers receive a thorough understanding of the subject matter. Thanks for engaging with the text. If you would like to know more, feel encouraged to connect with me by means of any social network. I am excited about your questions. In summing up, for additional information, provided here are a selection of related write-ups that are likely engaging:Happy learning!