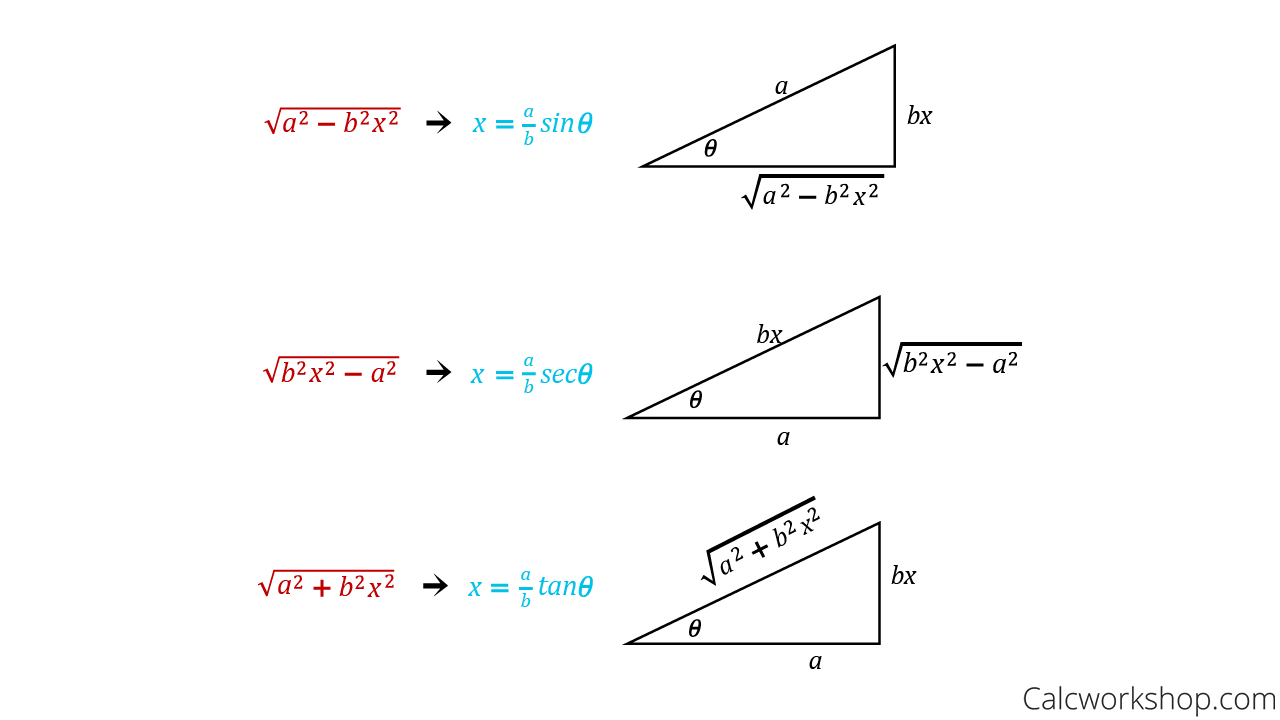
Trig Substitution Your New Best Friend In Calculus Solution: in this example we'll use a combination of u substitution and trigonometric substitution. very often, a u sub is possible, but other measures are needed to complete the integration. very often, a u sub is possible, but other measures are needed to complete the integration. This integral involves a very interesting trigonometric substitution. $\int[\ln(x)\arcsin(x)] dx$. it is one of the few integrals which contain a logarithmic and an inverse trig function. it is an interesting one. $\int \sin(x)\arctan(\sqrt{\sec(x) 1}) dx$. once again, another interesting trigonometric substitution.
Trigonometric Substitution Examples Solutions Videos Section 7.3 : trig substitutions. as we have done in the last couple of sections, let’s start off with a couple of integrals that we should already be able to do with a standard substitution. ∫x√25x2 − 4dx = 1 75(25x2 − 4)3 2 c ∫ x √25x2 − 4 dx = 1 25√25x2 − 4 c. both of these used the substitution u = 25x2 − 4 and at. Use our trig substitution table, and substitute x = tan(u). as written in the notes: 1 x2 = 1 tan 2 (u) = 1 cos 2 (u) in exercises for algebra of derivatives we calculated the derivative of tan(x) using the product rule: dx = 1 cos 2 (u) du the two go very well together: 1 (1 x 2 ) dx = cos 2 (u) dx = du easy to integrate: ∫1 (1 x 2. We have since learned a number of integration techniques, including substitution and integration by parts, yet we are still unable to evaluate the above integral without resorting to a geometric interpretation. this section introduces trigonometric substitution, a method of integration that fills this gap in our integration skill. Trigonometric substitutions are a specific type of u u substitutions and rely heavily upon techniques developed for those. they use the key relations \sin^2x \cos^2x = 1 sin2 x cos2 x = 1, \tan^2x 1 = \sec^2x tan2 x 1 = sec2 x, and \cot^2x 1 = \csc^2x cot2 x 1 = csc2 x to manipulate an integral into a simpler form.
Comments are closed.