Trigonometric Substitution Example 1

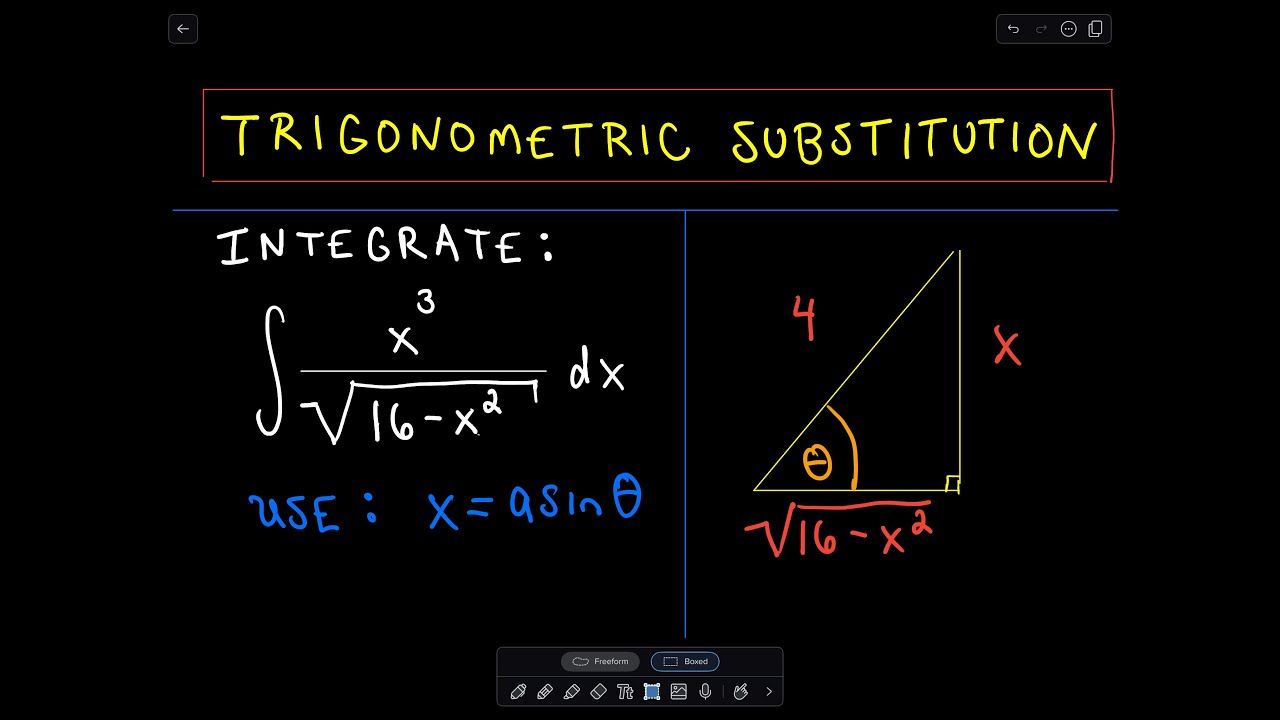
Trigonometric Substitution Example 1 Youtube Section 7.3 : trig substitutions. as we have done in the last couple of sections, let’s start off with a couple of integrals that we should already be able to do with a standard substitution. ∫x√25x2 − 4dx = 1 75(25x2 − 4)3 2 c ∫ x √25x2 − 4 dx = 1 25√25x2 − 4 c. both of these used the substitution u = 25x2 − 4 and at. Figure 7.3.7: calculating the area of the shaded region requires evaluating an integral with a trigonometric substitution. we can see that the area is a = ∫5 3√x2 − 9dx. to evaluate this definite integral, substitute x = 3secθ and dx = 3secθtanθdθ. we must also change the limits of integration.

Trigonometric Substitution Examples Solutions Videos Example \(\pageindex{5}\): using trigonometric substitution. evaluate \( \int\frac1{x^2 1}\ dx\). solution. we know the answer already as \(\tan^{ 1}x c\). we apply trigonometric substitution here to show that we get the same answer without inherently relying on knowledge of the derivative of the arctangent function. We may also use a trigonometric substitution to evaluate a definite integral, as long as care is taken in working with the limits of integration: we will evaluate. ∫1 −1 dx (1 x2)2. ∫ − 1 1 d x (1 x 2) 2. for this triangle, tan θ = x tan θ = x, so we will try the substitution x = tan θ x = tan θ. then θ = tan−1(x) θ = tan. Recall that if $$ x = f(\theta) \ , $$ $$ dx = f'(\theta) \ d\theta $$ for example, if $$ x = \sec \theta \ , $$ then $$ dx = \sec \theta \tan \theta \ d\theta $$ the goal of trig substitution will be to replace square roots of quadratic expressions or rational powers of the form $ \ \displaystyle \frac{n}{2} \ $ (where $ \ n \ $ is an integer. Trigonometric substitution example 1. just a basic trigonometric substitution problem. i show the basic substitutions along with how to use the right triangle to get back to the original variable. trigonometric substitution example 2. a complete example integrating an indefinite integral using a trigonometric substitution involving tangent.

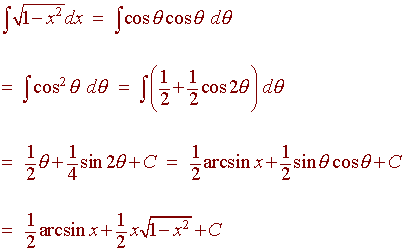
Trigonometric Substitution Recall that if $$ x = f(\theta) \ , $$ $$ dx = f'(\theta) \ d\theta $$ for example, if $$ x = \sec \theta \ , $$ then $$ dx = \sec \theta \tan \theta \ d\theta $$ the goal of trig substitution will be to replace square roots of quadratic expressions or rational powers of the form $ \ \displaystyle \frac{n}{2} \ $ (where $ \ n \ $ is an integer. Trigonometric substitution example 1. just a basic trigonometric substitution problem. i show the basic substitutions along with how to use the right triangle to get back to the original variable. trigonometric substitution example 2. a complete example integrating an indefinite integral using a trigonometric substitution involving tangent. The denominator of the integrand includes a difference of squares. this should encourage us to try a trigonometric substitution. the form is \( a^2 x^2 \), which reminds us of the trigonometric identity \( 1 \sin^2 \theta = \cos^2 \theta \). Table of trigonometric substitutions example 1 evaluate . solution let , where . then and (note that because .) thus, the inverse substitution rule gives cot c y csc2 1 d y cos2 sin2 d y cot2 d y s9 x2 x2 dx y 3 cos 9 sin2 3 cos d cos 0 2 2 s9 x2 s9 9 sin2 s 9 cos2 3 cos 3 cos x 3 sin 2 2 dx 3 cos d y s9 x2 x2 dx 2, 2 x a sin y f x dx y f t t t.

Trigonometric Substitution Example 1 Youtube The denominator of the integrand includes a difference of squares. this should encourage us to try a trigonometric substitution. the form is \( a^2 x^2 \), which reminds us of the trigonometric identity \( 1 \sin^2 \theta = \cos^2 \theta \). Table of trigonometric substitutions example 1 evaluate . solution let , where . then and (note that because .) thus, the inverse substitution rule gives cot c y csc2 1 d y cos2 sin2 d y cot2 d y s9 x2 x2 dx y 3 cos 9 sin2 3 cos d cos 0 2 2 s9 x2 s9 9 sin2 s 9 cos2 3 cos 3 cos x 3 sin 2 2 dx 3 cos d y s9 x2 x2 dx 2, 2 x a sin y f x dx y f t t t.